皆さん,こんにちは.こんばんは.🐻です.
今回は数学の問題について記事を書いておきたい.
多分このブログで数学について書くのは初めてだ.
なぜ解こうと思ったのか
$$\cos 20^\circ cos 40^\circ cos 80^\circ$$
↑をなぜ解こうと思ったのかについてであるが,理由は2つある.
1つ目の理由は,単位円を駆使すればなんとか解けるだろうという安直な思いがあったのにうまくいかず悔しいと思ってしまったからだ.(厨二病を拗らせた…)
2つ目の理由は,悔しくなって$$\cos 20^\circ cos 40^\circ cos 80^\circ$$の解き方を調べていると,英語のページに飛び,調べていくうちになんだか面白そうだと思ってしまったからだ.
ググってみた
分からない時はとりあえず,ググってみる.最近の私はダックり(duck duck go)気味だが…
すると英語の記事ではあるが,次の記事が見つかった.
$$\cos 20^\circ cos 40^\circ cos 80^\circ= \frac{ 1 }{ 8 }$$
結果は↑のようになる.
上のページで紹介されている解き方は,一見とてもシンプルに見えるが,途中で出てくるidentity(恒等式)が分からなかった.
一応,紹介されている解き方を記しておく.
To prove(証明)
$$\cos 20^\circ cos 40^\circ cos 80^\circ= \frac{ 1 }{ 8 }$$
Solution(解き方)
$$\cos 20^\circ cos 40^\circ cos 80^\circ$$を考える.
$$\cos 20^\circ cos 40^\circ cos 80^\circ$$
$$=\cos 40^\circ cos 20^\circ cos 80^\circ$$
$$=\cos40^\circ cos(60^\circ-20^\circ)cos(60^\circ+20^\circ)$$
Using the identity,(次の恒等式を使う)
$$\cos(60^\circ-A)cosAcos(60^\circ+A)= \frac{ 1 }{ 4 }cos3A \cdots (\ast)$$
$$(\ast)より$$
$$=\frac{ 1 }{ 4 }cos3(20^\circ)$$
$$=\frac{ 1 }{ 4 }cos60^\circ$$
$$=\frac{ 1 }{ 4 } \left(\frac{ 1 }{ 2 }\right)$$
$$=\frac{ 1 }{ 8 }$$
知らない恒等式(*)が登場
随分スッキリとした解き方だったが,何度も書くように初見では$$(*)$$がなぜ成り立つのか分からなかった.
$$\cos(60^\circ+A)cosAcos(60^\circ-A)= \frac{ 1 }{ 4 }cos3A \cdots (\ast)$$
外国人による(*)の詳しい解説
困ったなぁと思いながら,ネットサーフィンしていると,インド人(?)と思しき人がYouTubeを通じて手書きで説明していた.
ここでは動画で書かれていた証明をLaTeXを使って書き起こしをしておきたい.
$$\cos(60^\circ+A)cosAcos(60^\circ-A)= \frac{ 1 }{ 4 }cos3A$$を証明する。
$$(左辺)=\frac{ 1 }{ 2 }cosA2cos(60^\circ-A)cos(60^\circ+A)\cdots(a)$$
$$2cosAcosB=cos(A+B)+cos(A-B)$$より
$$(a)=\frac{ 1 }{ 2 }cosA[cos(60^\circ-A+60^\circ+A)+cos\{(60^\circ-A)-(60^\circ+A)\}]$$
$$=\frac{ 1 }{ 2 }cosA\{cos120^\circ+cos(-2A)\}\cdots(a)’$$
$$cos\theta=cos(-\theta)$$より
$$(a)’=\frac{ 1 }{ 2 }cosA(cos2A+cos120^\circ)$$
$$=\frac{ 1 }{ 2 }cosA(cos2A-\frac{ 1 }{ 2 })$$
$$=\frac{ 1 }{ 2 }cosA(\displaystyle \frac{2cosA-1}{2})$$
$$=\frac{ 1 }{ 4 }(2cosA\cdot cosA-cosA )\cdots(b)$$
$$2cosAcosB=cos(A+B)+cos(A-B)$$より
$$(b)=\frac{ 1 }{ 4 }\{cos(2A+A)+cos(2A-A)-cosA\}$$
$$=\frac{ 1 }{ 4 }(cos3A+cosA-cosA)$$
$$=\frac{ 1 }{ 4 }cos3A$$
よって$$\cos(60^\circ+A)cosAcos(60^\circ-A)= \frac{ 1 }{ 4 }cos3A$$ が示された.
まとめ
最後にまとめと書いてしまっているので,ザックリまとめを書いておきたい.
- 高校数学の範囲である筈なのに,問題の解法が分からず自分の出来の悪さに唖然とした.
- 調べていくうちに,日本語の記事は無かったが,海外の方による説明があって,助かった.数学は万国共通だということが感じられて,楽しかった.
- 調子に乗ってLaTeXを使ってみたのはいいけれど,とても疲れた.
- もう少しLaTeXに慣れていきたい.
- ダメダメな自分でも楽しめた数学に感謝したい.
【参考にしたページ】
MathJax で利用可能な T E X コマンド(非公式)
それでは.🐻でした.
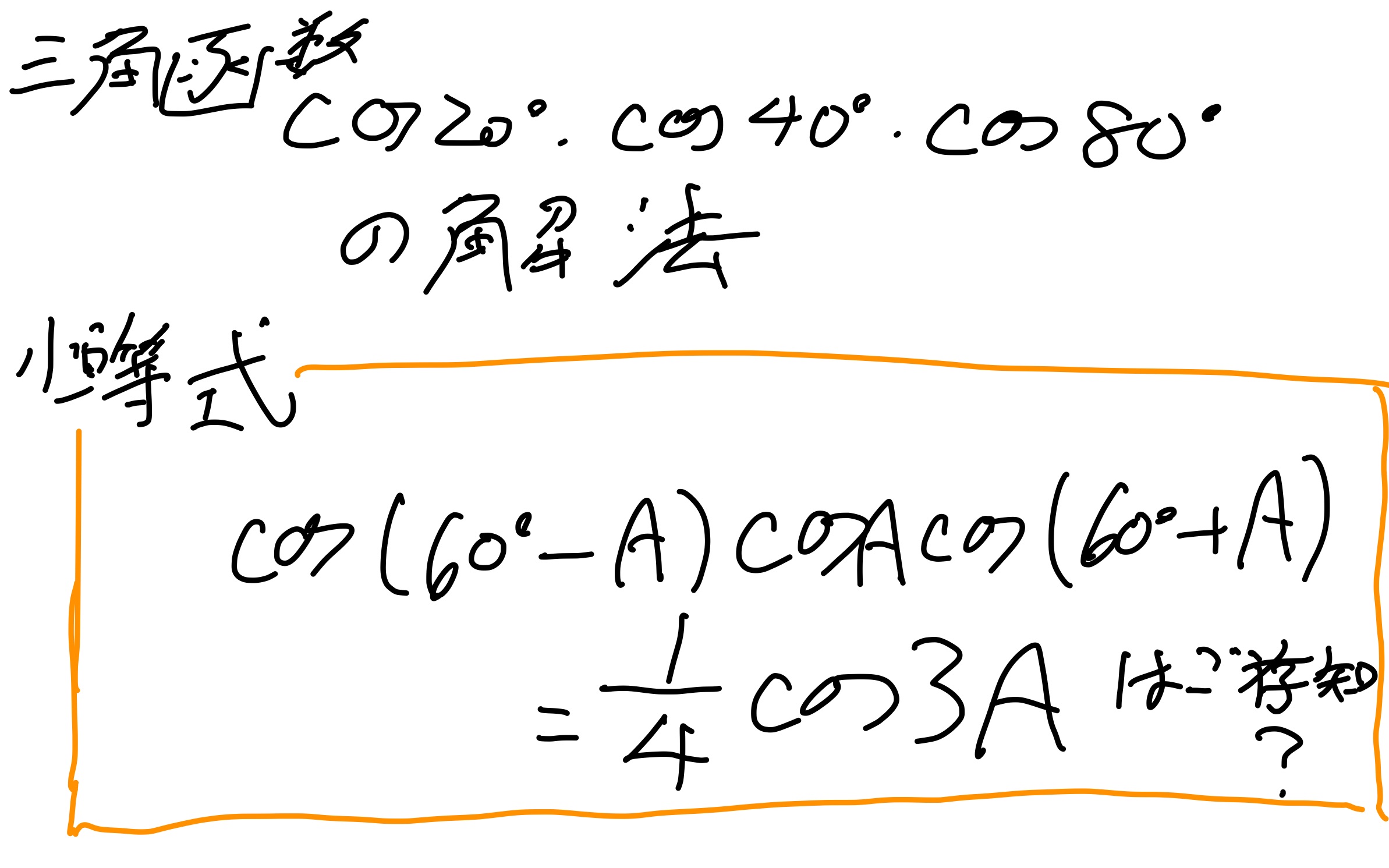


コメント
I every time used to read post in news papers but now as I am a user of web so from now I am using net for articles or reviews, thanks to web.|
We stumbled over here from a different web address and thought I may as well check things out. I like what I see so now i’m following you. Look forward to checking out your web page repeatedly.|
Unquestionably consider that which you stated. Your favourite reason seemed to be at the web the easiest thing to have in mind of. I say to you, I certainly get irked while other folks consider concerns that they plainly don’t know about. You managed to hit the nail upon the highest and defined out the entire thing with no need side-effects , folks can take a signal. Will probably be again to get more. Thank you|
It is perfect time to make some plans for the longer term and it’s time to be happy. I have learn this put up and if I may just I wish to suggest you some fascinating things or advice. Perhaps you could write subsequent articles relating to this article. I want to read more issues about it!|
Magnificent website. Lots of useful info here. I am sending it to a few friends ans also sharing in delicious. And of course, thanks for your sweat!|
Aw, this was an extremely good post. Taking the time and actual effort to create a good article… but what can I say… I hesitate a lot and never seem to get anything done.|
Hey there! Do you know if they make any plugins to protect against hackers? I’m kinda paranoid about losing everything I’ve worked hard on. Any suggestions?|
You can definitely see your expertise within the work you write. The world hopes for even more passionate writers like you who are not afraid to say how they believe. Always follow your heart.|
Long living the peace